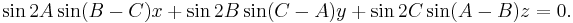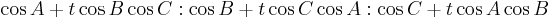Euler line

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral; it passes through several important points determined from the triangle. It passes through the orthocenter, the circumcenter, the centroid, and the center of the nine-point circle of the triangle.

Euler showed in 1765 that in any triangle, the orthocenter, circumcenter and centroid are collinear. This property is also true for the nine-point center, although it had not been defined in Euler's time. In equilateral triangles, these four points coincide, but in any other triangle they do not, and the Euler line is determined by any two of them. The center of the nine-point circle lies midway along the Euler line between the orthocenter and the circumcenter, and the distance from the centroid to the circumcenter is half that from the centroid to the orthocenter.

Other notable points that lie on the Euler line are the de Longchamps point, the Schiffler point, the Exeter point and the far-out point. However, the incenter lies on the Euler line only for isosceles triangles.

The Euler line is its own complement, and therefore also its own anticomplement.

Let A, B, C denote the vertex angles of the reference triangle, and let x : y : z be a variable point in trilinear coordinates; then an equation for the Euler line is

$\sin 2A \sin(B - C)x %2B \sin 2B \sin(C - A)y %2B \sin 2C \sin(A - B)z = 0.\,$

Another particularly useful way to represent the Euler line is in terms of a parameter t. Starting with the circumcenter (with trilinears 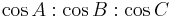$\cos A�: \cos B�: \cos C$ ) and the orthocenter (with trilinears 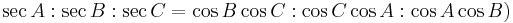$\sec A�: \sec B�: \sec C = \cos B \cos C�: \cos C \cos A�: \cos A \cos B)$ , every point on the Euler line, except the orthocenter, is given as

$\cos A %2B t \cos B \cos C�: \cos B %2B t \cos C \cos A�: \cos C %2B t \cos A \cos B\,$

for some t.

Examples:

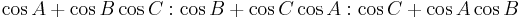
centroid = $\cos A %2B \cos B \cos C�: \cos B %2B \cos C \cos A�: \cos C %2B \cos A \cos B$
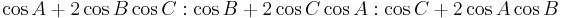
nine-point center = $\cos A %2B 2 \cos B \cos C�: \cos B %2B 2 \cos C \cos A�: \cos C %2B 2 \cos A \cos B$
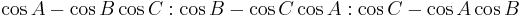
De Longchamps point = $\cos A - \cos B \cos C�: \cos B - \cos C \cos A�: \cos C - \cos A \cos B$
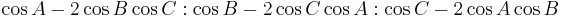
Euler infinity point = $\cos A - 2 \cos B \cos C�: \cos B - 2 \cos C \cos A�: \cos C - 2 \cos A \cos B$

References

Euler, Leonhard (1767). "Solutio facilis problematum quorundam geometricorum difficillimorum". Novi Commentarii academiae scientarum imperialis Petropolitanae 11: 103–123. E325. http://math.dartmouth.edu/~euler/pages/E325.html. Reprinted in Opera Omnia, ser. I, vol. XXVI, pp. 139–157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953, MR 0061061.

Kimberling, Clark (1998). "Triangle centers and central triangles". Congressus Numerantium 129: i–xxv, 1–295.

External links

Altitudes and the Euler Line and Euler Line and 9-Point Circle at cut-the-knot
Triangle centers on the Euler line, by Clark Kimberling.
An interactive applet showing several triangle centers that lies on the Euler line.
Weisstein, Eric W., "Euler Line" from MathWorld.
"Euler Line" by Eric Rowland, the Wolfram Demonstrations Project, 2007.
Nine-point conic and Euler line generalization at Dynamic Geometry Sketches Generalizes nine-point circle to a nine-point conic with an associated generalization of the Euler line.